JSYoo94

[ Rubust CNN-based Gait Verification and Identification using SGEI ]

( 1 ) ........ [ SGEI ] Skeleton Extraction & Gait Period Analysis ( 현재글 )

  이 논문에서는 보행자의 Skeleton을 OpenPose Network를 통해 얻어낸 후 , 보행자의 다리를 하나의 Pendulum으로 가정하고 회전 각을 계산하여 Gait Period ( 보행 주기 ) 를 계산한다. 이후 한 주기 동안의 Silhouette Image들과 Skeleton을 이용하여 SGEI를 만들어낸다. 이를 통해 보행자의 옷, 들고있는 물건 등의 외형 변화에 따른 영향을 제거하는 것이 목표이다.

- Skeleton Extraction

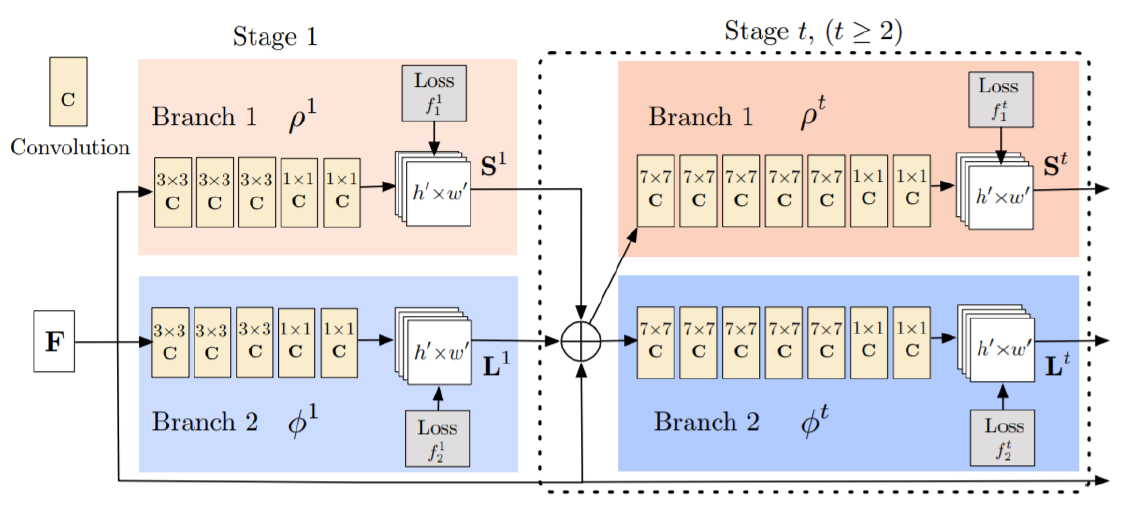
  먼저 위 그림은 OpenPose Network의 Architecture이다. 2개의 Branch로 구성되어 있고 Stage를 직렬로 연결한다. 하나의 Branch는 Part Confidence Maps을, 다른 Branch는 Part Affinity Fileds를 예측하는 구조이다. 본 논문에서는 OpenPose Network에 대한 자세한 설명을 생략하겠다. 그에 관한 내용은 아래 링크를 참고하면 좋을 것 같다.

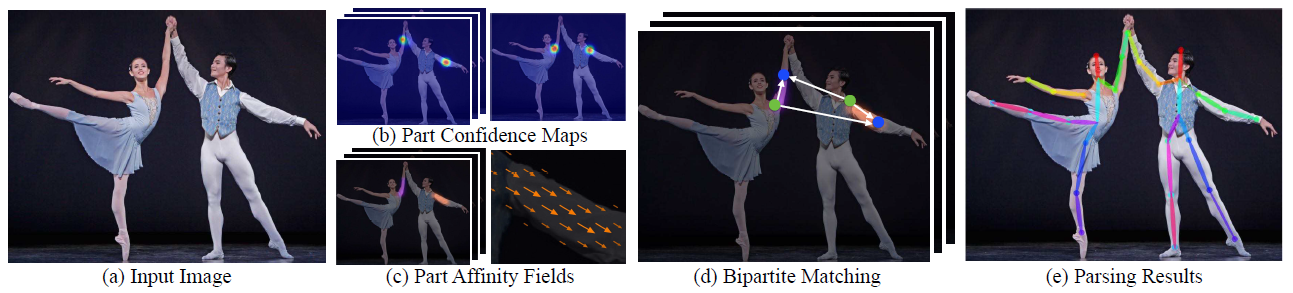
○ OpenPose : https://blog.naver.com/worb1605/221297566317

- Gait Period Analysis

  입력으로 들어오는 개개인의 Gait Sequence는 길이가 각각 다를 수 있다. 찍힌 시점에 따라 시작 Frame에 Gait Cycle이 시작될 수도 있고, Gait Cycle의 중간부터 시작해서 이어질 수도 있다. 동일한 조건에서 Gait Feature를 뽑아내야 유리하기 때문에, 한 주기를 측정하기 위해 보행자의 다리를 Pendulum으로 가정한 후 각도를 이용한다.

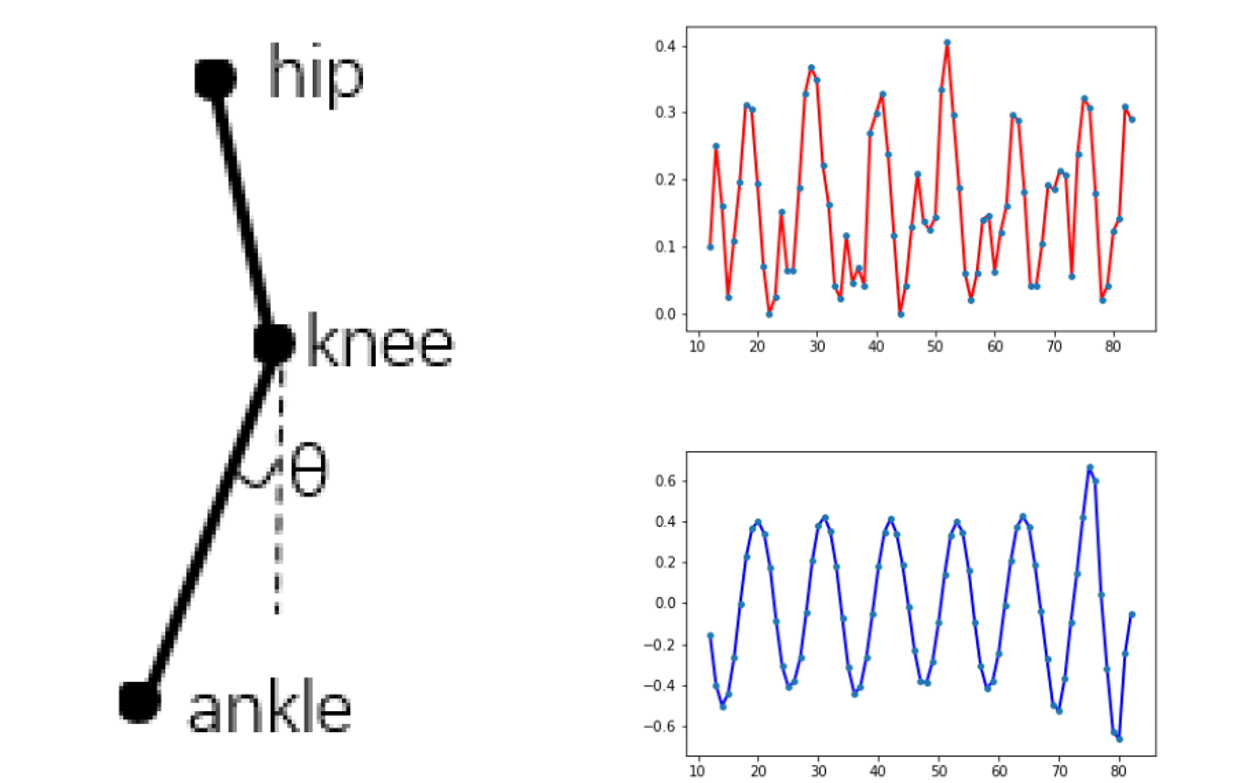
  위 그림을 보면, 다리를 하나의 Pendulum으로 가정한 후, 무릎에서 발목까지의 Vector와 무릎에서 지면으로의 수직 Vector사이의 각도를 측정하여 오른쪽 위의 Signal을 만들어 낸다. 

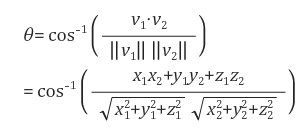
  위 수식을 통해 Vector 사이의 각을 구할 수 있다. 하지만 이렇게 뽑아낸 Signal Graph만 보고 Gait Period를 측정하는 건 쉽지 않다. 따라서 논문에서는 normalization, mean filtering, autocorrelation등의 과정을 통해 오른쪽 아래의 파란 Signal을 만들어 내었다. 그 과정은 아래와 같다.

○ Normalization

  먼저 평균 (mean) 값으로 빼준 후 Standard deviation으로 normalization하면 된다. 직접 CASIA-B Dataset을 통해 진행해본 결과는 아래와 같다.

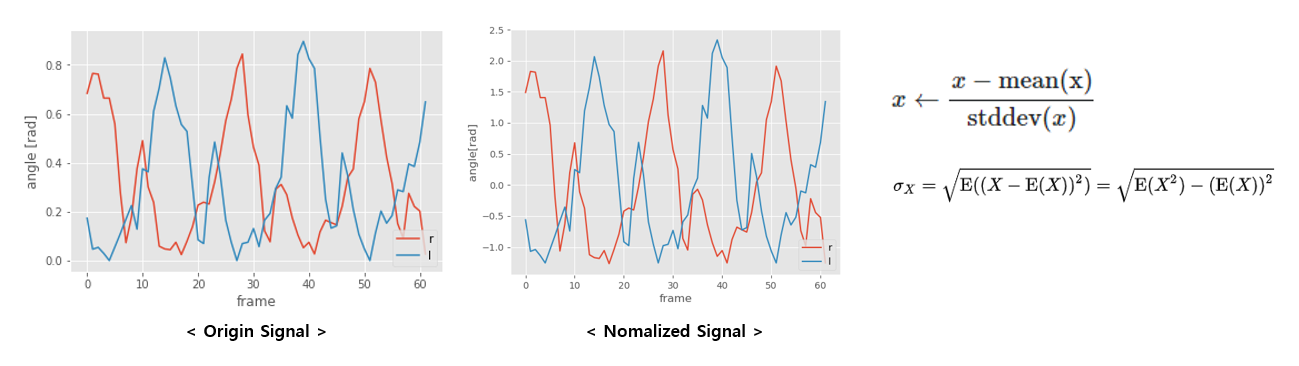
○ Mean Filtering

  다음으로 평균 Filter를 통과시킨다. 정해진 크기의 window를 움직여가면서 window 내의 값을 평균하여 출력하는 Filter이다. Edge에서의 처리에 따라 결과가 다른데, 주변 값을 활용하여 Extension해주거나 Periodic Signal의 경우 그냥 반대편에서 Data를 가져다 ( 앞 부분엔 뒤의 Data, 뒷 부분엔 앞 쪽의 Data, 환형 Queue를 생각하면 쉬울 듯 ) 쓰는 경우도 있다. 하지만 앞서 말한대로 어떤 Gait Cycle 동작에서 시작할 지 모르므로, 그냥 채워주지 않고 사용했다.

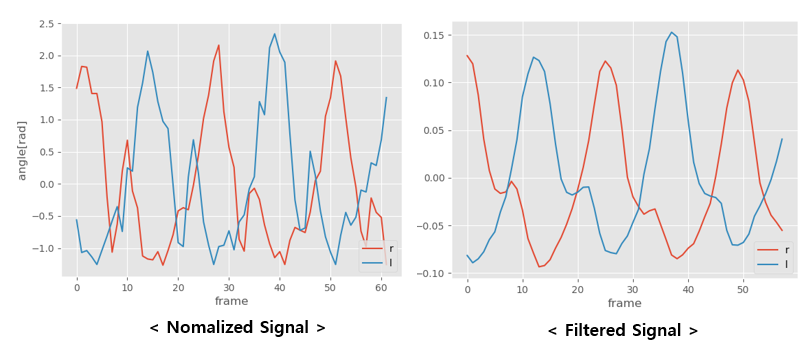
○ Autocorrelation

  마지막 단계는 Autocorrelation이다. correlation이란 두 Signal 사이의 상관성을 따져볼 때 사용되는 개념이다. 시계열 Data에서는 현재의 상태가 과거 또는 미래의 상태와 연관지어 생각할 수 있는 경우가 많다. 이럴 때, 시간 이동된 자기 신호화의 상관성을 Autocorrelation이라고 한다.

  몇 가지 주요한 특징이 있는데,

     1. Autocorrelation은 대칭적이다.

     2. 원점에서 최고점에 도달

     3. 주기적 SIgnal은 그 주기성을 유지한다.

  시간 이동된 자기 신호화의 상관성을 따질 수 있기 때문에, Peak만 찾으면 주기를 알 수 있게 되고, 주기성을 유지하기 때문에 더욱 좋다.

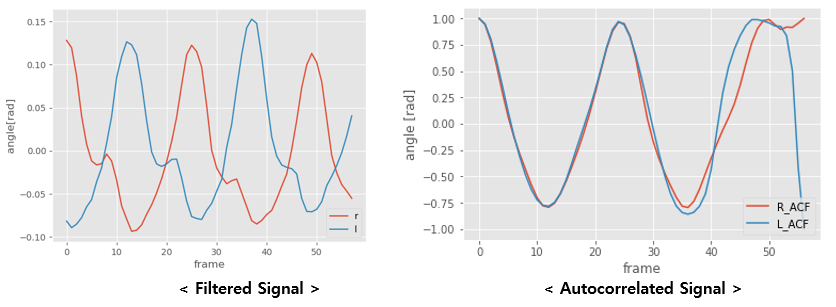
  오른쪽의 Graph를 보면 오른쪽, 왼쪽 다리를 각각 계산해 보았을 때의 Graph이다. Peak부터 Peak까지의 Frame 수를 주기로 생각하고 사용할 수 있다.

- SGEI

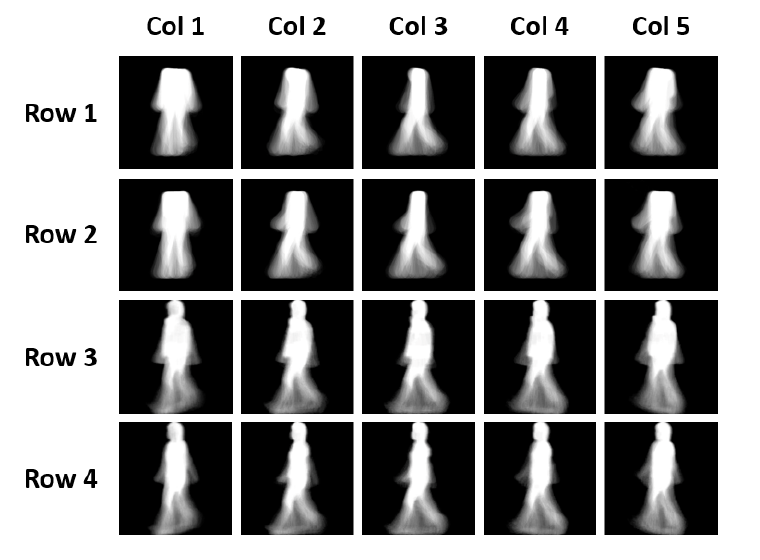
  위 그림의 1, 2 Row는 SGEI 3, 4 Row는 GEI를 나타낸다. SGEI를 만들 때에는 Skeleton Extraction을 통해 얻어낸 Body Part Point에 17 pixel radius의 원을 그리고 Body Part 간의 연결을 35 pixel의 width를 가진 Rectengle로 Skeleton을 그린 후 한 주기의 Silhouette Image를 입력으로 받아 SGEI를 만들어낸다.

  다음 글에서는 SGEI를 이용해 Gait Verification 과 Identification을 하는 과정에 대해 알아보겠다.

- 참고자료

- Robust CNN-based Gait Verification and Identification using Skeleton Gait Energy Image

- OpenPose : Realtime Multi-Person 2D Pose Estimation using Part Affinity Fileds

[ GaitSet : Regarding Gait as a Set for Cross-View Gait Recognition]

( 1 ) ........ Gait as Unordered Set

( 2 ) ........ Proposed Method & Set Pooling ( 현재 글 )

( 3 ) ........ Horizontal Pyramid Mapping & Multilayer Global Pipeline

- Proposed Method

  위 그림은 전체적인 GaitSet Model의 구조를 나타낸 것이다. Gait을 set으로 다루기 위해서 Concept을 수식화하면 아래와 같다.

  N명의 Dataset이 주어졌을 때, 각 사람의 Gait silhouette들이 어떤 Distribution을 따른다고 가정한다. 이때 각 분포는 해당 사람의 Identity에만 연관되어 있다. 그렇다면 한 사람의 여러 Gait Sequence를 하나의 큰 set으로 생각할 수 있다. 이러한 가정을 토대로 수식을 세우면 위 왼쪽 수식과 같다.

  F 는 Convolutional Network를 의미하고, 각 Silhouette Image의 Frame Level Feature Extraction을 목적으로 한다. G는 Permutation invariant function으로 Frame Level Feature를 하나의 Set Level Feature로 추합해주는 함수이다. Set Pooling으로 구현되어 있고 설명은 아래 단락에서 하겠다. 마지막으로 H는 Horizontal Pyramid Mapping을 통해 구현되었는데, 한 사람의 보행 Data 분포를 잘 구분지을 수 있도록 표현하는 Representation을 학습하기 위한 함수이다. HPM은 다음 글에 적도록 하겠다.

- Set Pooling

  Set 단위의 입력을 주었을 때,  각각의 Silhouette Image에서 직접적으로 Feature Extraction이 이루어진다. 이 때 추출된 Local Feature를 Frame Level Feature라고 표현한다. 입력 Image 갯수 만큼의 Local Feature를 추출한 뒤 이 Feature들을 Aggregation하여 Global Feature인 Set Level Feature를 만들어내는 구조이다. 이 때, Local Feature Aggregation 방법으로 논문에서는 Set Pooling이라는 방식을 제안하였다. 

  위 그림을 보면 Set Pooling을 G( · ), z = Set Level Feature, V = Frame Level Feature 로 수식화했다. 이때 두 가지의 제약 조건이 있다.

  첫 번째로 입력이 set 단위이기 때문에 ( 중복을 허용하지 않고, 순서가 없다. ) 공식화된 G는 Permutation invariant function이어야 한다. Permutation invariant의 뜻은, 입력 Vector의 요소 순서와 상관 없이 같은 출력을 내는 것을 말합니다. 즉 G( · )는 입력의 순서에 상관없이 요소가 같은 입력이라면 같은 출력을 내는 함수여야 합니다. 대표적인 예로 MLP ( Multi Layer Perceptron )를 들 수 있다.

  두 번째로 실제 상황에서는 사람의 Gait Silhouette의 숫자가 항상 동일하지 않을 수 있다. 따라서 G( · )는 임의의 cardinality로 Set을 취할 수 있어야 한다. 여기서 cardinality라는 단어에서 살짝 당황했는데, 위키피디아와 다른 글을 참고하자면 사전적 의미로는 집합원의 갯수를 의미하고, 상대적 개념으로 보면 중복도의 높고 낮음을 나타내는 지표이다.

예를 들어 집합 A = {0, 1, 2, 3, 4}의 Cardinality는 5이고 , B = { 남, 남, 여, 여, 여 }의 Cardinality는 2이다. 상대적으로 봤을 때 A의 Cardinality가 B보다 높다고 표현할 수 있다.

  쉬운 이해를 위해 다른 예를 들자면, 한국의 지역 집합에는 우리나라 여러 지명이 들어있을 것이고, 주민번호 집합에는 개개인의 주민번호가 담겨있을 것이다. 상대적으로 주민번호 집합이 Cardinality가 높다고 표현할 수 있다. 유한 집합의 경우에는 자연수로 표현할 수 있지만, 무한 집합의 크기는 자연수로 표현할 수 없고 상대적인 크기를 표현할 때 사용한다.

  여튼 결과적으로 두 번째 제약의 의미는, Set의 길이다. 위의 그림에서 알 수 있듯이 Cardinality가 높을 수록, 즉 Sequence의 길이가 길수록 성능이 좋아짐을 알 수 있다.

  위 두 제약조건을 만족시키기 위해 Statistical Function을 Set dimension에 적용한다. Computational Cost와 Representativeness를 고려하여 max( · ), mean( · ), median( · )의 3가지 함수를 적용한다. 이 함수들을 적절히 사용하여 Joint Function의 형태로 G( · )를 구성한다.

  최근 Visual Attention이 많은 분야에서 성공적으로 적용되고 있기 때문에, 이를 포함한 Set Pooling Layer를 구성한다. 위의 그림이 이를 표현한 그림이다. Main idea는 Global Information을 활용하여 element-wise attention map을 학습시키고 이를 통해 frame-level feature map을 정제하는 것이다.

이전글 ) GaitSet : Gait as Unordered Set

다음글 ) GaitSet : Horizontal Pyramid Mapping & Multilayer Global Pipeline

- 참고 자료

- GaitSet : Regarding Gait as a Set for Cross-View Gait Recognition, Hanqing Chao et al arXiv:1811.06186

[ GaitSet : Regarding Gait as a Set for Cross-View Gait Recognition]

( 1 ) ........ Gait as Unordered Set ( 현재 글 )

( 2 ) ........ Proposed Method & Set Pooling

( 3 ) ........ Horizontal Pyramid Mapping & Multilayer Global Pipeline

- Gait as Unordered Set

  일반적으로 Gait Recognition에서 Gait ( 보행 ) 은 크게 두 가지 방법으로 표현된다. 하나는 Image로, 한 Sequence의 Gait Silhouette Image 들을 하나의 Image로 압축하여 표현하는데 대표적으로 GEI ( Gait Energy Image), CGI ( Chrono Gait Image), PEI ( Period Energy Image ) 등이 있다.

  위 방법의 최대 장점은, 먼저 구현하기 쉽고, Data를 다루기 쉬우며, Cost가 낮다는 점이다. 하지만 순간적이고 세밀한 공간 정보를 쉽게 잃는다는 단점이 있다. 따라서 최근에는 Gait Sequence의 Silhouette Image들에서 직접적으로 Feature를 뽑아내는 방식에 대한 연구가 진행되고 있다. 이러한 방식은, 각 Frame에서의 Feature를 직접 추출하기 때문에 그 순간의 세밀한 정보를 보존할 수 있다는 장점이 있다. 하지만 해당 Image에 Noise가 포함되어 있는 경우 굉장히 취약해진다. 또 Network에 더 많은 Memory를 필요로 할뿐더러, 학습하기도 어렵다는 단점이 있다.

  이 논문에서는 이러한 두 방법의 문제를 해결하기 위해 Set 단위의 Gait Sequence를 사용하는 색다른 방법론을 제안한다.

  보행은 주기적인 운동으로 단일 기간 내에서 나타낼 수 있다. 이때, 한 주기의 Gait Sequence를 임의로 섞는다 하더라도, 각각의 Gait Image의 시간적 위치가 어디였는지 알아볼 수 있을 충분히 독특한 특징이 있기 때문에 이 논문에서는 Set 단위의 Gait Sequence를 사용한다.

  즉, 각 Silhouette Image의 형태에는 해당 Image의 시간적 Position에 대한 정보가 포함되어 있다고 가정한다. 그렇다면, Gait Sequence의 순서는 더 이상 중요하지 않게 되고, 각 Image에서 직접 Feature를 추출할 수 있게 된다.

이러한 방법의 장점을 크게 세 가지로 표현하자면 아래와 같다.

1. Flexible

  Network의 입력에 어떠한 제약 조건도 없기 때문에 유연하다는 장점이 있다. 하나의 Set을 구성하는 Gait Sequence의 길이에 제한이 없고, Viewpoint, Walking Condition 등과 같은 외적 요인도 상관 없이 입력으로 줄 수 있다.

2. Fast

  GaitSet Model은 한 쌍의 Gait Template ( Sequence ) 간 유사도를 측정할 필요가 없이 Gait Representation을 직접적으로 학습한다. 따라서 각 Sample의 Representation은 단 한번만 계산하면 되고, Recognition 시 Representation 간 거리를 측정하면 된다. 이로 인해 빠르다는 장점이 있다.

3. Effective

  GaitSet model은 CASIA-B Dataset 과 OU-MVLP Dataset에서 굉장한 성능 향상을 이루었다. Viewpoint와 Walking Condition의 변화에 강한 특성을 보여주었다.

다음글 ) GaitSet : Proposed Method & Set Pooling

  다음 글에서는 논문에서 사용된 다른 기법 Set Pooling 과 Horizontal Pyramid Mapping에 대해 정리해보겠다.

- 참고 자료

- GaitSet : Regarding Gait as a Set for Cross-View Gait Recognition, Hanqing Chao et al arXiv:1811.06186